10800. Прямоугольники

Имеется набор n квадратов со стороной 1. Сколько разных прямоугольников можно сформировать из этих квадратов?

Два прямоугольника считаются разными, если ни один из них нельзя повернуть и переместить, чтобы получить второй. Во время построения прямоугольника нельзя ни деформировать квадраты, ни накладывать их на другие.

Вход. Одно целое число n (1 ≤ n ≤ 10⁹).

Выход. Выведите количество различных прямоугольников, которые можно образовать из квадратов.

Пример входа	Пример выхода
6	8

РЕШЕНИЕ

перебор

Анализ алгоритма

Пусть i * j (i ≤ j) – размер прямоугольника, который можно составить из квадратов. Поскольку i ≤ j и i * j ≤ n, то i ≤ .

Переберем меньшую сторону прямоугольника i от 1 до . Переберем вторую сторону прямоугольника j от i до тех пор пока i * j ≤ n. В переменной cnt подсчитываем число таких пар (i, j).

cnt = 0;

for (i = 1; i <= sqrt(n); i++)

for (j = i; i * j <= n; j++)

cnt++;

Второй цикл можно свернуть в формулу. Можно заметить, что j в нем пробегает от i до n / i. То есть значение cnt на i-ой итерации будет увеличено на n / i – i + 1. Приведенный двойной цикл можно переписать следующим образом:

cnt = 0;

for (i = 1; i <= sqrt(n); i++)

cnt = cnt + (n / i - i + 1);

Пример

Рассмотрим первый тест n = 6. Меньшая сторона прямоугольника перебирается от 1 до = 2.

Для i = 1 вторая сторона j может принимать значения от i = 1 до n / i = 6. Имеем 6 прямоугольников:

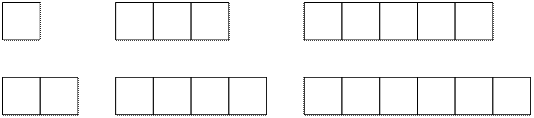
Для i = 2 вторая сторона j может принимать значения от i = 2 до n / i = 3. Имеем два прямоугольника:

Итого для n = 6 имеется 8 возможных прямоугольников.

Реализация алгоритма

Читаем входное значение n.

scanf("%d", &n);

Вычисляем ответ.

cnt = 0;

for (i = 1; i <= sqrt(n); i++)

cnt = cnt + (n / i – i + 1);

Выводим ответ.

printf("%lld\n", cnt);

Python реализация

import math

Читаем входное значение n.

n = int(input())

Вычисляем ответ.

cnt = 0

for i in range(1, int(math.sqrt(n)) + 1):

cnt += (n // i - i + 1)

Выводим ответ.

print(cnt)